卷积神经网络
卷积神经网络CNN
卷积神经网络的英文全称为Convolutional Neural Network,它是一类强大的、为处理图像数据而设计的神经网络,是一种深度的监督学习下的机器学习模型。基于卷积神经网络架构的模型在计算机视觉领域中已经占主导地位,应用于目标检测、边缘检测、语义分割、图像描述、问答系统、风格迁移等场景。
特征学习阶段
图像卷积(卷积层)
卷积层是个错误的叫法,因为它所表达的运算其实是互相关运算(cross-correlation)。下面动图很好的展示了图像卷积的过程。首先我们需要有一个卷积核(Kernel或Filter),对于图像上的一个点,让模板的原点和该点重合,然后模板上的点和图像上对应的点相乘,然后各点的积相加,就得到了该点的卷积值。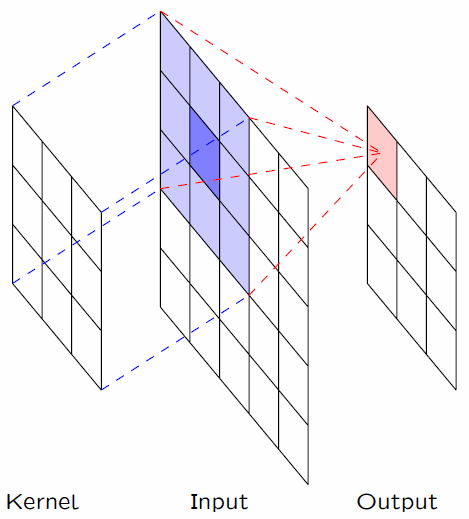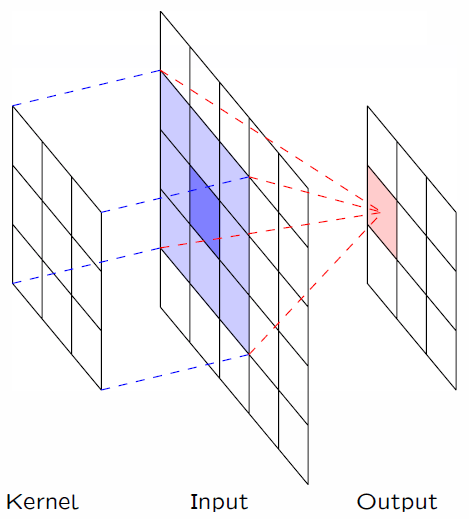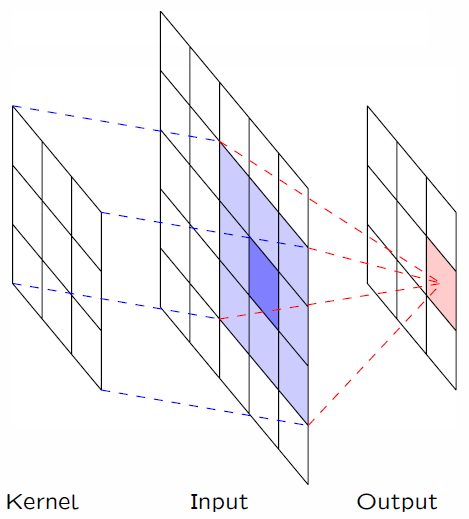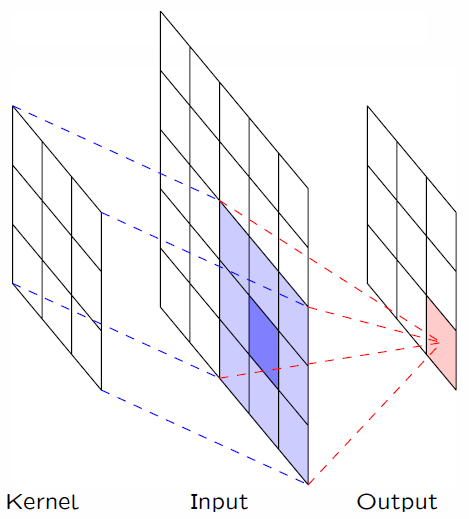
举例一个处理二维图像数据的例子(暂时不考虑三维)。下面我们输入一个高度是3、宽度是3的二维张量(形象的表达是一个3*3的矩阵)。卷积核的高度和宽度都是2。
输出的卷积层有时被称为特征映射(feature map),因为它可以被视为一个输入映射到下一层的空间维度的转换器。
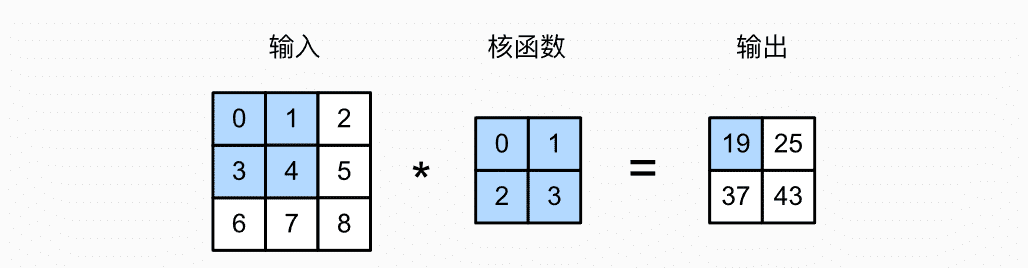
从[[0,1],[3,4]]开始与卷积核计算。计算完向右移动一个格子,[[1,2],[4,5]]—>[[3,4],[6,7]]—>[[4,5],[7,8]]
阴影部分是第一个输出元素:
0 * 0+ 1 * 1+3 * 2 + 4 * 3=19
其余输出元素:
1 * 0+ 2 * 1+4 * 2 + 5 * 3=25
3 * 0+ 4 * 1+6 * 2 + 7 * 3=37
4 * 0+ 5 * 1+7 * 2 + 8 * 3=19
从上面我们可以看到被选中蓝色的部分每次先向右移动一次,当移动到最边缘时,从开始部位向下移动再向右移动。当没有声明步幅时默认是1,也可以进行人为的修改。
步幅(Stride)
在计算互相关时,卷积窗口从输入张量的左上角开始,向下、向右滑动。上述例子默认移动一个元素。为什么会引出步幅呢?这是为了实现高效计算或缩减采样的次数。卷积窗口可以跳过中间位置,每次滑动多个元素。步幅分为水平步幅和垂直步幅。
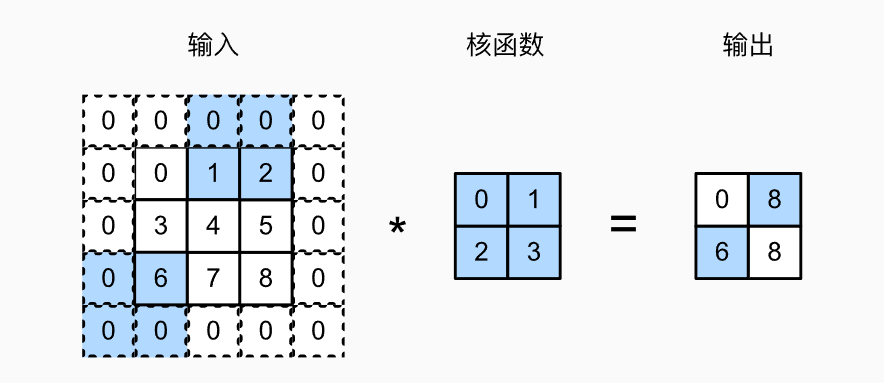
上图是垂直步幅为3,水平步幅为2的二维互相关运算。 着色部分是输出元素以及用于输出计算的输入和内核张量元素:
0 * 0 + 0 * 1 + 1 * 2 + 2 * 3 = 8
0 * 0 + 6 * 1 + 0 * 2 + 0 * 3 = 6
可以看到,为了计算输出中第一列的第二个元素和第一行的第二个元素,卷积窗口分别向下滑动三行和向右滑动两列。但是,当卷积窗口继续向右滑动两列时,没有输出,因为输入元素无法填充窗口(除非我们添加另一列填充)。
如果观察仔细,可以看到我们在原33的矩阵周围加了一圈0元素,让他变成了55的矩阵。这个操作叫做填充。
填充(Padding)
在应用多层卷积时,我们常常丢失边缘像素。 由于我们通常使用小卷积核,因此对于任何单个卷积,我们可能只会丢失几个像素。 但随着我们应用许多连续卷积层,累积丢失的像素数就多了。所以引出了填充的方法:在图像便捷填充元素(通常为0,也可以复制图像边界填充)。
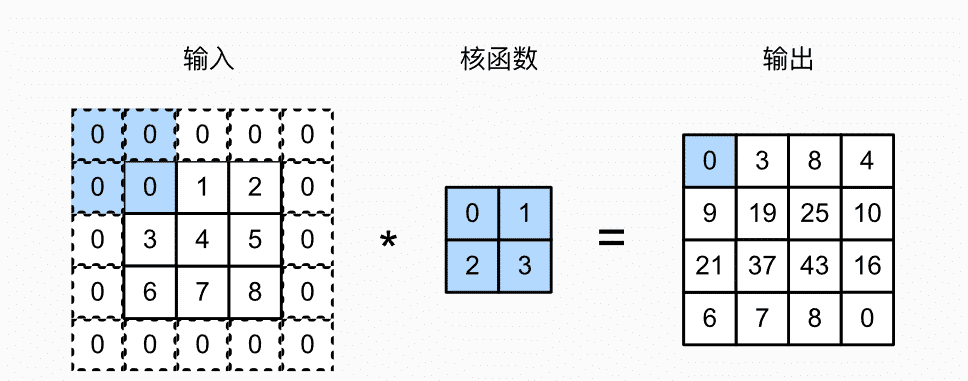
我们将3 * 3输入填充到5 * 5,那么它的输出就增加为4 * 4。阴影部分是第一个输出元素以及用于输出计算的输入和核张量元素:
0 * 0+ 0 * 1 + 0 * 2 + 0 * 3 = 0。
总结
填充就是在图像边界添加一圈新的元素,步幅就是每次移动长度。
多输入、多输出图像(Depth)
上述例子中是单通道的卷积,但是生活中更多是多通道的图像,如:RGB。我们用i表示输入张量的通道数,用o表示输出张量的通道数,h和w分别为高和宽。
例如,每个RGB输入图像具有3 * h * w的形状。我们将这个大小为3的轴称为通道(channel)维度,也用Depth深度去表示。下图以双通道单输出为例,计算方式和单通道一样,分别计算再将两个通道的元素相加得到输出结果。
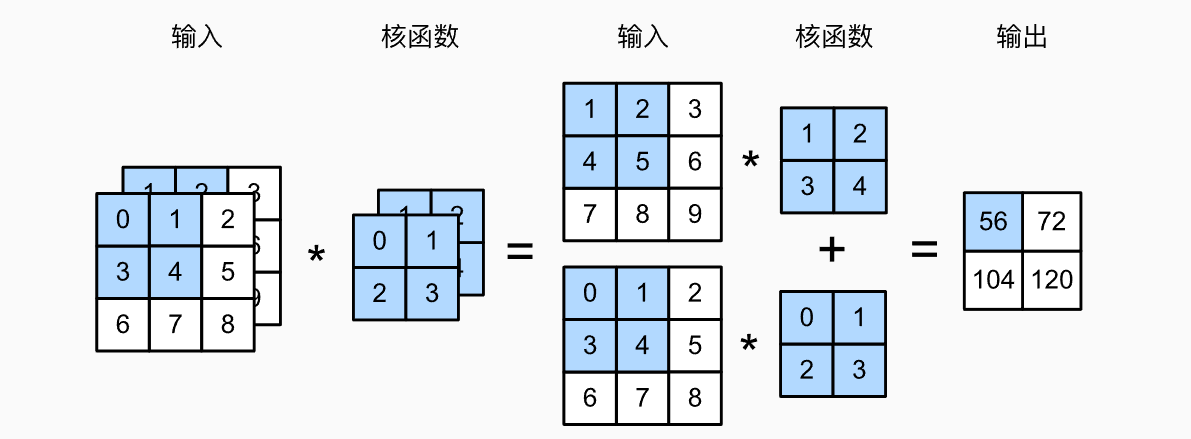
但是实际情况可能不会只有一个输出通道,当我们进行分类时,可能会将不同类别的元素进行归类,这就需要多通道来解决这个问题。
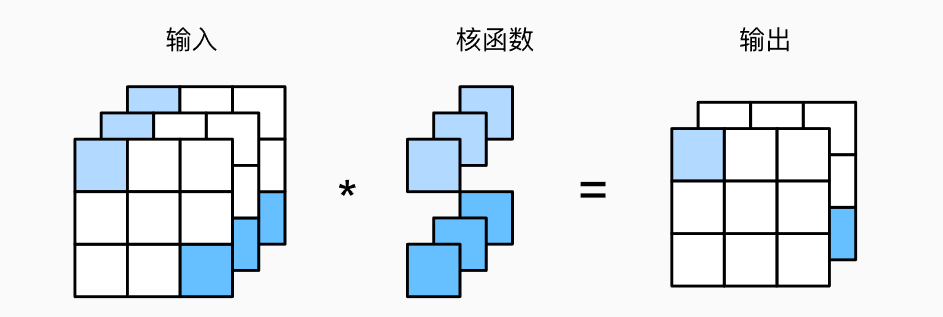
为了获得多个通道的输出,我们可以为每个输出通道创建一个形状为i * h * w的卷积核张量,这样卷积核(Kernel)的形状是o * i * h * w。
激活函数
卷积层后面常常跟RELU层,该层主要目的在于引入非线性计算单元,RELU函数如下:
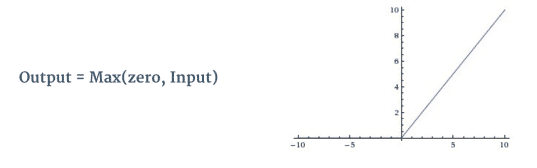
ReLU 是一种单个像素操作,并将特征图中的所有负值替换为零。 ReLU 的目的是在我们的 ConvNet 中引入非线性,因为我们希望训练的 ConvNet 学习的大多数现实世界数据都是非线性的(卷积是一种线性运算——元素矩阵乘法和加法,所以我们通过引入非线性函数(如 ReLU)来解释非线性。
上述左侧为应用RELU操作前效果图,右侧为应用RELU操作后效果图.
汇聚层
池化层或称汇聚层(Pooling)操作主要用于卷积层或特征图的维数减少,保留相对重要信息。有时这种空间池化也称为下采样。池化层可以分为最大池化、平均池化、和池化。通常情况下,最大池化层使用最多。
与卷积层类似,汇聚层运算符由一个固定形状的窗口组成,该窗口根据其步幅大小在输入的所有区域上滑动,为固定形状窗口(有时称为汇聚窗口)遍历的每个位置计算一个输出。 然而,不同于卷积层中的输入与卷积核之间的互相关计算,汇聚层不包含参数。 相反,池运算是确定性的,我们通常计算汇聚窗口中所有元素的最大值或平均值。这些操作分别称为最大汇聚层(maximum pooling)和平均汇聚层(average pooling)。
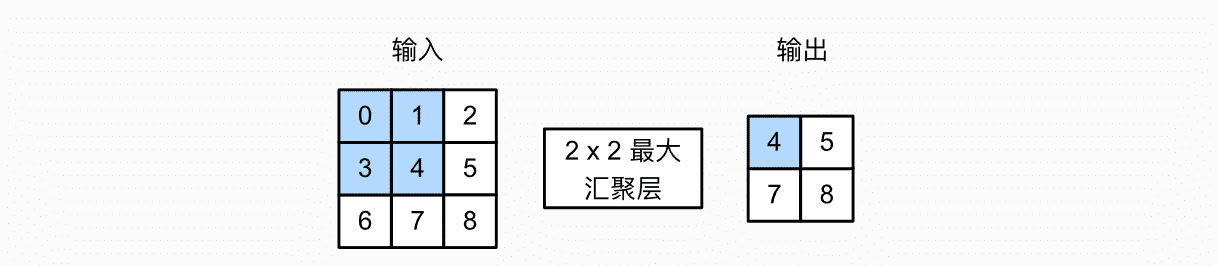
上图是最大汇聚层,输出每个汇聚窗口的最大值:
max(0,1,3,4) = 4
max(1,2,4,5) = 5
max(3,4,6,7) = 7
max(4,5,7,8) = 8
平均汇聚层是将汇聚窗口的所有元素求平均,在输出。
分类阶段
这里我们主要使用了全连接层(fully connected layers,FC),全连接层是传统的多层感知器,在输出层使用了 Softmax 激活函数。“全连接”意味着前一层的每个神经元都连接到下一层的每个神经元。
卷积层和池化层的输出代表输入图像的高级特征。全连接层的目的是使用这些特征根据训练数据集将输入图像分类为各种类别,可以理解成“分类器”的作用。
全连接层的输出概率之和为 1,主要通过在全连接层的输出层使用 Softmax 作为激活函数来确保的。 Softmax 函数采用任意实值作为输入,并将其压缩为介于 0 和 1 之间且总和为 1的值 。
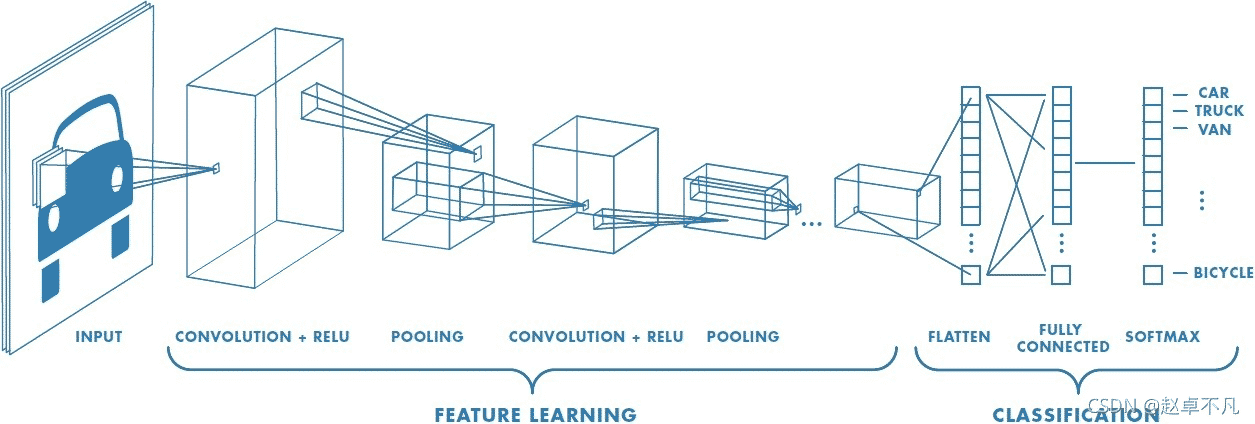
在上图中,对全连接层使用 softmax 给出了汽车、卡车和自行车等类别的概率值。
参考文章链接:https://blog.csdn.net/sgzqc/article/details/120544978
推荐一本宝藏学习机器学习的书:
序言 — 动手学深度学习 2.0.0-beta0 documentation (d2l.ai)
关于CNN的学习,推荐一个知乎专栏: