形态学图像处理

形态学简介

形态学（morphology）是原生物学的专业分支，主要研究的是动植物的形态与结构。在1964年，数学形态学诞生于法国巴黎，1968年成立法国枫丹白露数学形态学研究中心是，它是以形态为基础对图像进行分析的数学工具。90年代至今，数学形态学在模式识别，编码，运动分析，运动景物描述等方面取得进展，
用于数值函数的形态学算子开发。

$\textcolor{RubineRed}{具体一点，我们以数学形态学为工具，从图像中提取表达和描绘区域形状的有用的图像分量，如边界、骨架等。}$

集合论

形态学的语言是集合论，处理图像时，数学形态学中的集合表示图像中的目标。

元素和集合

一幅图像称为一个集合，集合也称样本空间$\Omega $。$\textcolor{BurntOrange}{对于二值图像，可认为取值为1的点对应于图像前景像素，取值为0的点对应于背景。} $

（1）集合元素的运算

集合的基本运算总共有 4 种，分别是交、并、差、补。

a. 交运算

对于集合A、B，交运算（Intersection）被定义为：

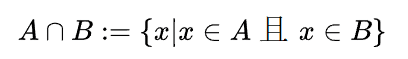
b. 并运算

对于集合A、B，并运算（Union）被定义为：

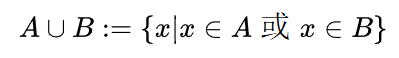
c. 补运算

集合A的补集是不包含于集合A的元素所组成的集合，表示为：

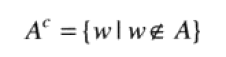
d. 差运算

对于集合A、B，差运算（Relative Complement）被定义为：

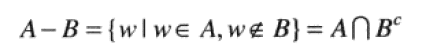
可以看出，这个集合中的元素属于A，而不属于B。我们可根据$\Omega $集合差值运算来定义$A^c$，即$A^c$=$\Omega $ - A。

下面是一些公式；

（2）形态学的运算

二值形态学中的运算对象是集合，在图像处理中，$\textcolor{OrangeRed}{我们使用两类像素集合的形态学：}$

a 目标元素：前景像素的集合

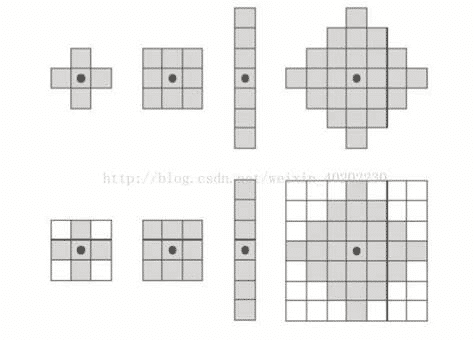
b 结构元（SE）：可以按照前景像素和背景像素来规定